Kodeclik Blog
Finding Tangent Lines of Cubic Functions
Finding the tangent line of a cubic function involves a systematic process that combines calculus concepts with algebraic manipulation.
Derivative of a function
The derivative of a function serves as a powerful tool for finding the slope of the tangent line at any point on a curve. While the derivative itself is not the tangent line, it provides the exact measurement of the tangent line's slope at any given point.
Think of it this way: when you calculate the derivative f'(x) of a function f(x), you're creating a new function that can tell you the slope of the tangent line at any x-value. For instance, if you want to know the slope of the tangent line at x = 1, you simply compute f'(1), and if you need the slope at any other point, you just plug that x-value into the derivative function.
This relationship is fundamental in calculus and helps us understand how a function changes at any particular point. When a function is increasing, the derivative (and thus the tangent line's slope) is positive; when decreasing, the derivative is negative; and at local maximum or minimum points, the derivative equals zero, resulting in a horizontal tangent line.
Derivative of a cubic curve
Let us consider the cubic curve:
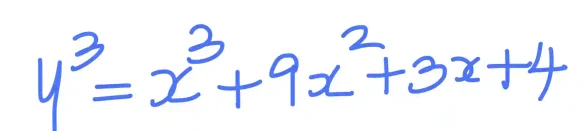
Let us plot this curve using Desmos:
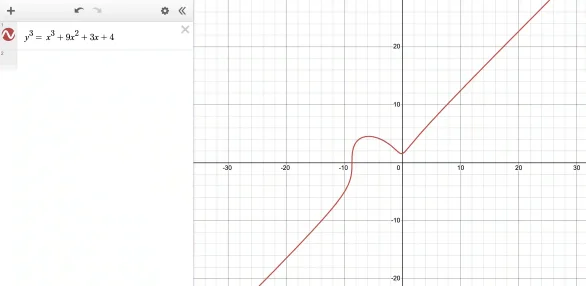
What is the derivative of this curve? To do that we first write out an explicit form for y as a function of x:

The derivative is then given by:
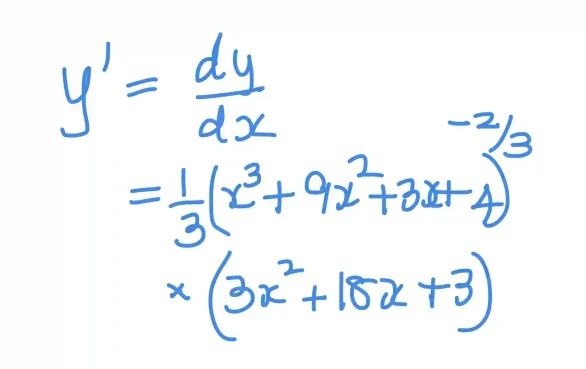
Let us plot this curve on top of y already plotted:
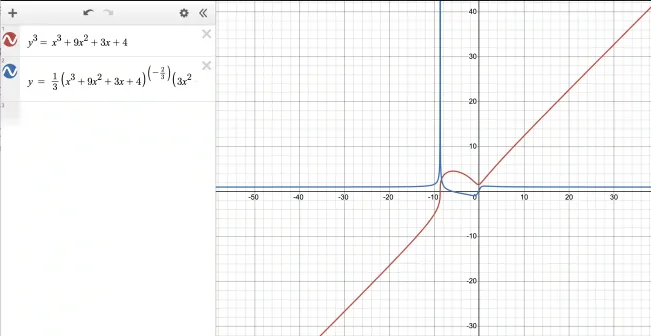
Note that the derivative is not the tangent line but gives us a measurement of what the slope (of the tangent) will be at any given point. Next, we show how to use this information to find the tangent at a given point.
Finding the tangent at x=0
Let us suppose we wish to find the values of m and b such that y = mx+b is a tangent to this curve at, say, x = 0.
At x=0, the derivative is given by (substitute x=0 in the derivative equation above) y’=0.39865. Now since y=mx+b is the tangent line to the curve at the point (x=0), it must be on the curve at this point, so y must be (substitute x=0 in the equation for the function above) 4^(⅓). How did we get this? We simply substituted x=0 in y^3 = x^3+9x^2+3x+4, which gives us y^3 = 4. So we now know that (0, 4^(⅓)) lies on this line. Substitute these values in y=mx+b and you will get b=4^(⅓). What is m? Note that m is the slope of the line which is just the value of the tangent, which is 0.39865.
Thus, the line that describes the tangent is y=0.39865x + 4^(⅓). Let us plot this in Desmos and see!
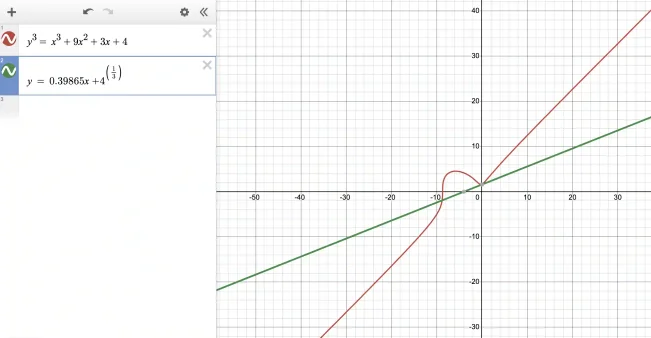
As you can see the line we have constructed is a perfect tangent at the point x=0 to our original curve. (We have blanked out the derivative curve as it will confuse the plot and make it look crowded.)
Finding the tangent at x=-10
Let us redo this exercise for x=-10. In other words, we wish to find the values of m and b such that y = mx+b is a tangent to this curve a x=-10.
At x=0, the derivative is given by (substitute x=0 in the derivative equation above) y’=1.63131. Now since y=mx+b is the tangent line to the curve at the point (x=-10), it must be on the curve at this point, so y must be (substitute x=-10 in the equation for the function above) -5.0133. Again the way we got this is by simply substituting x=-10 in y^3 = x^3+9x^2+3x+4.
So we now know that (-10, -5.0133) lies on this line. Substitute these values in y=mx+b remembering that m is the slope of the line which is just the value of the tangent, which is 1.63131. So we get: y = 1.63131x + 11.2998.
Again let us plot this in Desmos!
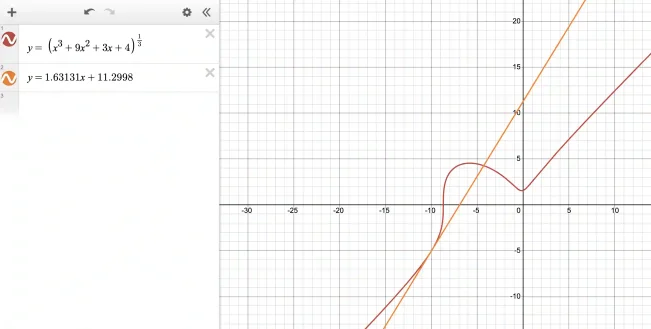
As you can see the tangent is now tangent at x=-10.
Special cases: Horizontal Tangents and Normal Lines
A horizontal tangent occurs when the derivative equals zero. It is easy to find them again by simply taking the derivative of your original curve and setting it equal to zero.
A normal line is perpendicular to the tangent line at the point of tangency. Its slope is the negative reciprocal of the tangent line's slope.
In summary, the derivative gives the slope of the tangent line at any point. You can always verify that the point lies on the original curve. The tangent line touches the curve at exactly one point and the above process works for any cubic function regardless of its complexity!
If you liked this blogpost and would like more experience with Desmos, learn how to make a heart shape with Desmos! Also learn about more geometric designs in Desmos!
If you enjoyed this blogpost, learn about math quadrants next! Explore Kodeclik’s Math courses and bootcamps! For more math fun, checkout our blog post on generating random numbers and on 100+ middle school math games.