Kodeclik Blog
Is there a “reverse” factorial?
We know what a factorial is, right? A factorial is simply the product of all positive integers less than or equal to a given number.
For instance, the factorial of 3 is 6 (3 × 2 × 1). The factorial of 4 is 24 (4 × 3 × 2 × 1). By convention, the factorial of 0 is 1.
But what do we mean by reverse factorial? Or say a factorial inverse?
The inverse factorial of x refers to the number y such that y’s factorial is x. In other words, you wish to find a number whose factorial is your given number.
Unlike the factorial function, it is not guaranteed that the reverse of the factorial will lead to an integer.
For instance, the inverse factorial of 6 is 3. But what is the inverse factorial of 5? The below figure shows some inverse factorial values.
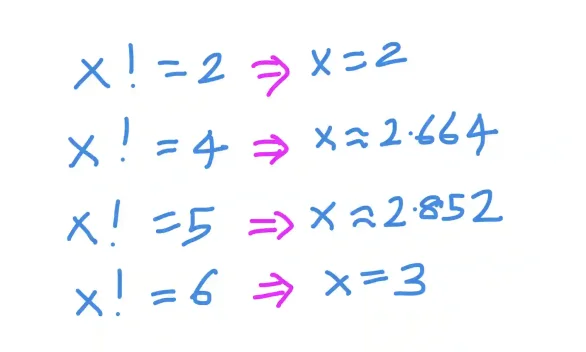
You can think of the inverse factorial as an “undo” for the factorial. What does it mean to say that the inverse factorial of 5 is 2.852? It is clear it has to be really close to 3, because the inverse factorial of 6 is 3, but how did we arrive at 2.852?
Essentially, the problem is: if you are given a positive number x, how can you find a number y such that y! = x, or perhaps y! Is approximately equal to x?
Before we show you the magic calculations, let us first try to find the two integers whose factorial will book-end your given number. Lets write a Python program to do so!
Python program to reverse the factorial function
Here's a Python program to find the inverse factorial of a number, which will either find such a number if it exists or find the two integers whose factorials bookend the given number:
import math
def find_inverse_factorial(x):
if x < 1:
return "Input must be positive"
# Start with n = 1 and keep calculating n! until we exceed x
n = 1
factorial = 1
while factorial <= x:
n += 1
factorial *= n
lower_bound = n - 1
upper_bound = n
lower_factorial = factorial // n
if x == lower_factorial:
return f"Exact inverse factorial of {x} is {lower_bound}"
else:
return f"Number {x} lies between {lower_bound}! ({lower_factorial}) and {upper_bound}! ({factorial})"
# Test cases
for i in range(2,10):
print(find_inverse_factorial(i))The program starts by taking a number and calculating factorials in ascending order until it finds a factorial equal to or larger than the input number. It maintains two variables: n (the current number being “factorial-ed”) and factorial (the running product).
Once it exits the while loop, the program identifies two important values: the lower bound (the integer corresponding to the previous factorial) and upper bound (integer corresponding to the current factorial). These bounds effectively "sandwich" our input number, telling us where it falls in the sequence of factorials. Even though the factorial value has gotten over-written, we can divide it by n to get the “lower factorial”.
Finally, we check if the given number is the same as the lower factorial in which case we found an exact inverse factorial. Else, we have found a range and so we print that range.
The output will be:
Exact inverse factorial of 2 is 2
Number 3 lies between 2! (2) and 3! (6)
Number 4 lies between 2! (2) and 3! (6)
Number 5 lies between 2! (2) and 3! (6)
Exact inverse factorial of 6 is 3
Number 7 lies between 3! (6) and 4! (24)
Number 8 lies between 3! (6) and 4! (24)
Number 9 lies between 3! (6) and 4! (24)Looking at the output, we can see patterns emerge. For example, the numbers 3, 4, and 5 all lie between 2! (2) and 3! (6), while 7, 8, and 9 all lie between 3! (6) and 4! (24). Only certain numbers like 2 and 6 have exact inverse factorials, which is why they return "Exact inverse factorial" instead of a range.
Using Gamma Functions to reverse the factorial function
Now I am sure the above is a little bit unsatisfying. It would be great if we could hone in on a floating point value between our book-ends as we show in our figure earlier.
The mathematical details of how to do this is a little bit beyond the scope of this blogpost but it involves solving equations with Gamma functions. First, here is the code:
import math
from scipy.optimize import root_scalar
def inverse_factorial(n):
"""
Compute the inverse factorial of a given integer n using the Gamma function.
This function computes the floating-point value of k such that k! \u2248 n
by solving for k in the equation \u0393(k+1) = n, where \u0393 is the Gamma function.
Parameters:
n (int): The input number to find the inverse factorial for.
Returns:
float or None: The floating-point value k such that \u0393(k+1) \u2248 n,
or None if n is non-positive.
"""
if n <= 0:
return None # Factorials are defined for positive integers only.
# Define a function to solve \u0393(k+1) = n
def gamma_root(n):
# Define the target function \u0393(k+1) - n
def gamma_eq(k):
return math.gamma(k + 1) - n
# Use a root-finding method to solve \u0393(k+1) = n
result = root_scalar(gamma_eq, bracket=[1, n], method='brentq')
if result.converged:
return result.root
return None
return gamma_root(n)
# Example usage
if __name__ == "__main__":
for value in range(2, 10):
result = inverse_factorial(value)
print(f"The floating-point inverse factorial of {value} is {result:.5f}.")The Gamma function is like an extension of factorials to include decimals and fractions. While you don't need to know all the details of how the Gamma function works, the program above essentially uses it to check how close k comes to making k!=n. It tries out different values for k until it finds the best match, using a process called "root-finding," which involves narrowing down possible answers until it finds the one that works. The program then prints the result, showing k as a decimal number.
The output will be:
The floating-point inverse factorial of 2 is 2.00000.
The floating-point inverse factorial of 3 is 2.40587.
The floating-point inverse factorial of 4 is 2.66403.
The floating-point inverse factorial of 5 is 2.85236.
The floating-point inverse factorial of 6 is 3.00000.
The floating-point inverse factorial of 7 is 3.12108.
The floating-point inverse factorial of 8 is 3.22350.
The floating-point inverse factorial of 9 is 3.31210.This method is useful for exploring how factorials behave with numbers that aren't just simple whole numbers, opening the door to more advanced topics in math and science while staying rooted in the familiar idea of multiplication and factorials.
Where are inverse factorials used?
Inverse factorials are useful in math and science when we need to understand patterns or relationships that aren't restricted to whole numbers. For example, they help in probability calculations and models where smooth, continuous growth is essential. Even though the math behind functions like Gamma might seem complicated, the key idea is that it lets us work with fractional inputs in a way similar to factorials. Exploring inverse factorials is a great way to see how simple concepts like multiplication can lead to powerful ideas that apply to many areas of science and engineering.
Summary
The concept of inverse factorials is fascinating because it flips the usual question about factorials. Instead of asking, “What is n!?” we ask, “For a given number n, what value of k satisfies k!=n?” This is easy for small numbers where n is a perfect factorial, like 666 (where k=3k = 3k=3 because 3!=63! = 63!=6). However, when n is not a perfect factorial or is a decimal, we need a more advanced approach to solve for k. By using tools like the Gamma function, we can find not only whole numbers but also fractional or decimal values of k, giving us a smooth way to extend the idea of factorials beyond integers.