Kodeclik Blog
Lagrange’s Four-Square Theorem
Lagrange's four-square theorem, also known as Bachet's conjecture, states that every non-negative integer can be represented as the sum of four squared integers. This can be expressed mathematically as:
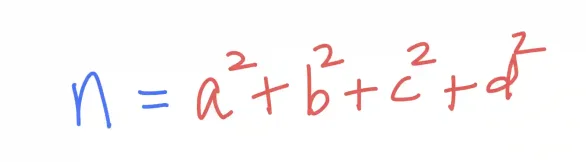
Here, a, b, c, and d are integers.
History of the Lagrange Four Square Theorem
The theorem's journey began in the 3rd century CE with Diophantus of Alexandria in his Arithmetica, though it wasn't until 1770 that Joseph-Louis Lagrange provided the first complete proof, despite Pierre de Fermat having discovered an earlier unpublished proof.
The theorem's significance extends beyond its initial formulation, connecting to various mathematical domains including quaternion algebra, Descartes' theorem of four "kissing circles," and the Ramanujan-Petersson conjecture. This remarkable theorem not only demonstrates that squares form an additive basis of order four but also serves as a cornerstone in additive number theory, leading to further developments such as Jacobi's formula for counting representations and Legendre's three-square theorem.
Python program to explore Lagrange’s Four Square Theorem
Here's a Python program that demonstrates Lagrange's Four Square Theorem by finding four squares that sum to each number from 1 to 25:
def find_four_squares(n):
# Try all possible combinations of four squares
for a in range(int(n ** 0.5) + 1):
for b in range(int((n - a*a) ** 0.5) + 1):
for c in range(int((n - a*a - b*b) ** 0.5) + 1):
d_squared = n - a*a - b*b - c*c
if d_squared >= 0:
d = int(d_squared ** 0.5)
if a*a + b*b + c*c + d*d == n:
return [a, b, c, d]
return None
# Print results for numbers 1 to 25
for num in range(1, 26):
squares = find_four_squares(num)
print(f"{num} = {squares[0]}² + {squares[1]}² + {squares[2]}² + {squares[3]}²")In the above program, the core function find_four_squares(n) employs a systematic approach using nested loops to iterate through possible combinations of squares. For each number from 1 to 25, it searches for four integers (a, b, c, d) whose squares sum to that number. The algorithm works by first calculating the maximum possible value for each variable using the square root of the remaining sum, then systematically testing combinations until a valid solution is found. For example, when finding squares for 7, it determines that 7 = 2² + 1² + 1² + 1².
The program uses a brute-force method, starting with the smallest possible squares and working upward, making it computationally simple for small numbers but potentially inefficient for larger values. Even though it uses four nested for loops (for a, b, c, and d) to search in a brute force fashion, the program tries to be a little bit smart. For a given value of a, it subtracts that square (offered by including a) and only tries values of b that fit within the remainder. In other words, it doesn’t deliberately create sums that are known to be larger than the given number.
The output is formatted to clearly show each number followed by its four-square decomposition, providing a practical verification of Lagrange's theorem for the first 25 positive integers:
1 = 0² + 0² + 0² + 1²
2 = 0² + 0² + 1² + 1²
3 = 0² + 1² + 1² + 1²
4 = 0² + 0² + 0² + 2²
5 = 0² + 0² + 1² + 2²
6 = 0² + 1² + 1² + 2²
7 = 1² + 1² + 1² + 2²
8 = 0² + 0² + 2² + 2²
9 = 0² + 0² + 0² + 3²
10 = 0² + 0² + 1² + 3²
11 = 0² + 1² + 1² + 3²
12 = 0² + 2² + 2² + 2²
13 = 0² + 0² + 2² + 3²
14 = 0² + 1² + 2² + 3²
15 = 1² + 1² + 2² + 3²
16 = 0² + 0² + 0² + 4²
17 = 0² + 0² + 1² + 4²
18 = 0² + 0² + 3² + 3²
19 = 0² + 1² + 3² + 3²
20 = 0² + 0² + 2² + 4²
21 = 0² + 1² + 2² + 4²
22 = 0² + 2² + 3² + 3²
23 = 1² + 2² + 3² + 3²
24 = 0² + 2² + 2² + 4²
25 = 0² + 0² + 0² + 5²The program is efficient for small numbers but may become slower for larger numbers due to its brute-force approach. For practical applications with larger numbers, more sophisticated algorithms would be needed.
Second Python program to explore Lagrange’s Four Square Theorem
If you look at the above output, another way to view the Lagrange Four Square Theorem is to say that a number is the sum of at most four perfect squares. “At most” here emphasizes the fact that sometimes a number can just be a perfect square itself, sometimes it can be a sum of two squares (thus, the square of the hypotenuse of a right triangle), and so on. So here is a Python program to systematically check for a given number which category it falls under:
def find_four_squares(n):
# Handle base cases
if n == 0:
return [0, 0, 0, 0]
# Check if number is perfect square
from math import isqrt
# Find first square
for a in range(isqrt(n) + 1):
if a * a == n:
return [a, 0, 0, 0]
# Find second square
for b in range(a, isqrt(n - a*a) + 1):
if a*a + b*b == n:
return [a, b, 0, 0]
# Find third square
for c in range(b, isqrt(n - a*a - b*b) + 1):
if a*a + b*b + c*c == n:
return [a, b, c, 0]
# Find fourth square
d = isqrt(n - a*a - b*b - c*c)
if a*a + b*b + c*c + d*d == n:
return [a, b, c, d]
return None # Should never reach here according to theorem
def main():
# Test the function with some numbers
test_numbers = [7, 23, 123, 999]
for num in test_numbers:
squares = find_four_squares(num)
print(f"\n{num} = ", end="")
terms = []
for i, sq in enumerate(squares):
if sq != 0:
terms.append(f"{sq}²")
print(" + ".join(terms))
# Verify the result
result = sum(x*x for x in squares)
print(f"Verification: {result} == {num}")
if __name__ == "__main__":
main()In this program, the find_four_squares(n) function takes a natural number n as input and returns a list of four numbers whose squares sum to n. The algorithm uses nested loops to try different combinations of squares, starting with the smallest possible values. As mentioned above, it checks if the number is a single perfect square, a sum of two squares, and so on.
When you run this program, it tests the given numbers i.e., [7, 23, 123, 999] and lists how they satisfy the four square theorem. The output will be:
7 = 1² + 1² + 1² + 2²
Verification: 7 == 7
23 = 1² + 2² + 3² + 3²
Verification: 23 == 23
123 = 1² + 1² + 11²
Verification: 123 == 123
999 = 1² + 1² + 6² + 31²
Verification: 999 == 999Applications of Lagrange’s Four Square Theorem
The theorem's practical value lies in its ability to break down complex numbers into simpler components, making it useful in scenarios where computational efficiency is crucial. For example, in computer graphics, calculating distances between points often involves squared terms, and the theorem helps optimize these calculations by providing efficient ways to decompose and process these values.
Another area where it is useful is in signal processing where inputs need to be decomposed into simpler components (like what we have done above).
If you liked this blogpost, checkout our blogpost on finding square roots in Python!
Want to learn Python with us? Sign up for 1:1 or small group classes.