Kodeclik Blog

Magic Square Generator

What is a magic square?

A magic square is a square grid of numbers such that adding up the numbers along rows, columns, or diagonals yields the same sum. A 3x3 magic square, for instance, is comprised of nine cells and here is an example magic square where the magic sum is 15.

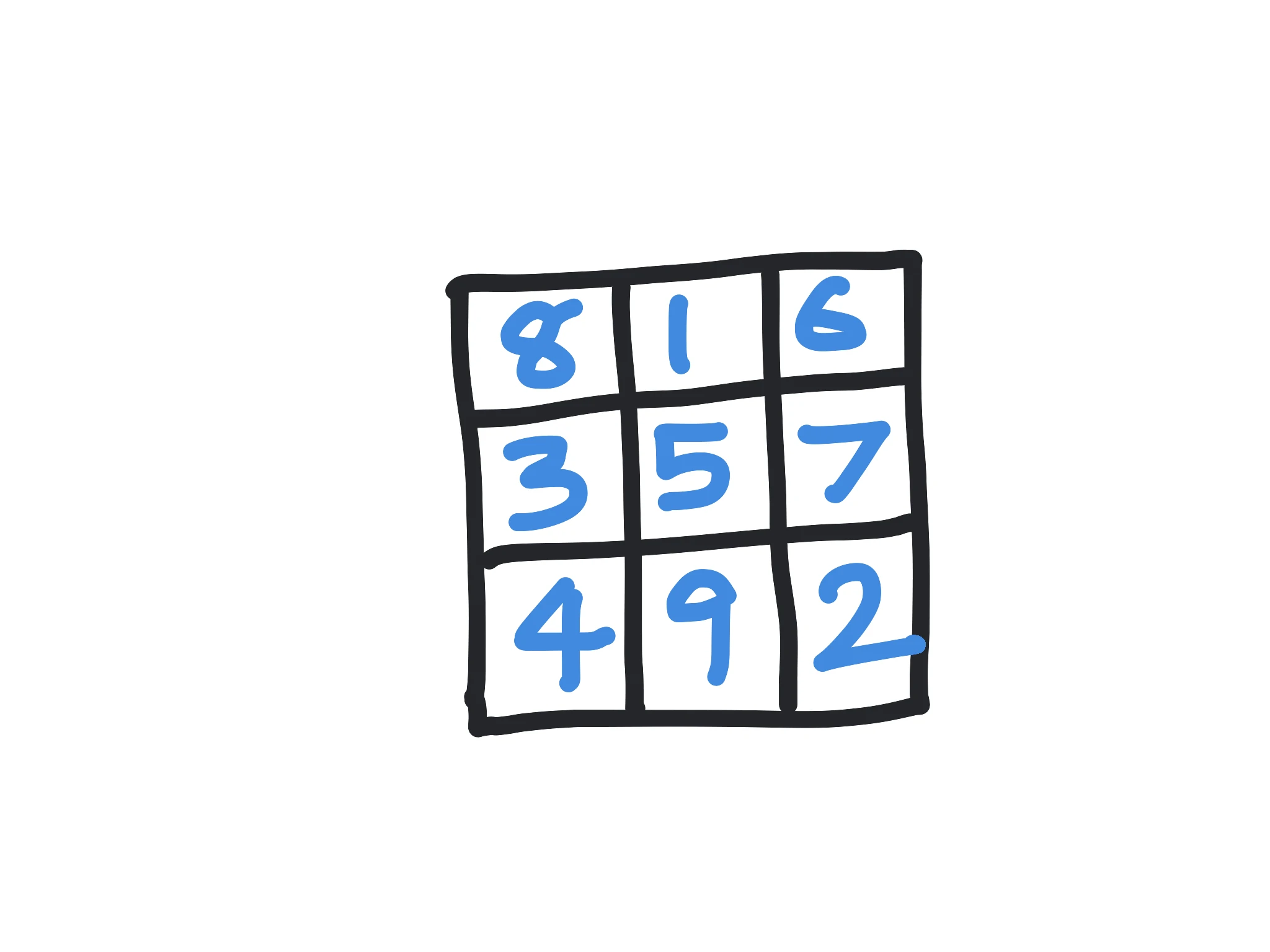
Where did magic squares come from?

Magic squares first appeared in Ancient China as early as 190 BC but only in the three by three variety. The concept then moved to India where four by four magic squares were constructed. Soon magic squares were a popular concept all around the world and so were the methods used to construct and solve them. Magic squares are still alive and popular today!

How do you make a magic square?

There are smart approaches that we can use to construct a magic square with consecutive numbers that we show later below in a Python program.

But a heuristic strategy is as follows. Simply pick a number (preferably a large one and let this be your magic sum. For our example below we will use a three by three magic square. Divide your number by three and place it in the middle cell. Next we will try out different numbers for the missing cells and keep switching them until we obtain a match. While this can be time consuming this is by far the most straightforward way.

How do you solve a magic square?

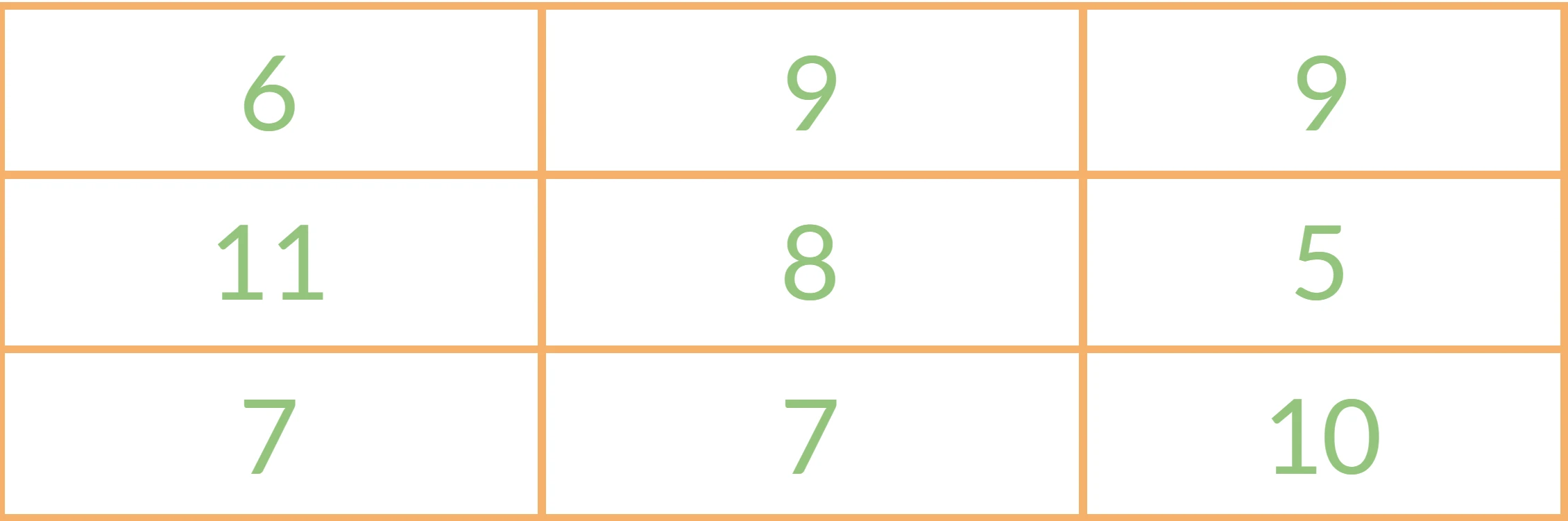
Solving a magic square means you are given some filled cells but other cells are unfilled, and your goal is to fill up all the given cells. You can use reasoning as well as trial and error to solve magic squares. We will walk you through how to solve the one below:

A good heuristic to solve magic square problems is to think of the middle cell which is part of many sums, along rows, columns, and diagonals. We can guess (and be right most of the time) that the middle cell will be a third of the magic sum. We can use this property to our advantage. We can call the middle cell “x”. From this we can construct the equation: x + 6 + 10 = 3x. From this we can deduce that x must be 8 and that the magic sum is 24.

Then we can continue with this magic sum in mind and fill in other cells to get the result as shown below:

Similar Concepts

There are a lot of concepts that are similar to the magic square such as the magic triangle. The magic triangle is composed of numbers along the edges all adding to the same number generally in the center of the triangle. There are also common math problems containing the idea of the magic square but not the shape.

Magic Square Generator in Python

To code a magic square generator we need to develop an algorithm first for making a magic square. We will show you one strategy, due to French diplomat de la Loubère. In honor of him, this method is called the de la Loubère method for constructing magic squares.

This method works only for magic squares of odd size, i.e., a 3-by-3, or 7-by-7. It will not work for magic squares of even size which need a different algorithm.

We begin the algorithm by placing the smallest number of the square in the first row, middle column. From that point onward we begin counting numbers incrementally and place them in successive cells.

How do you determine successive cells? The pattern is to look at the cell that is to the (right, above) with respect to the current cell. In other words, we move up one unit and to the right one unit.

In our current example, you will notice this takes us out of the square. In this case, we are still in a valid column but we have run out of rows. Because of this we will go down to the bottom row (keeping the same column) and put the next number in that spot.

Then we continue the process and place the next consecutive number in the cell that is to the (right, above) of the current cell. You will notice that we are again out of the square but this time we have run out of columns. So we will goto the first column (keeping the same row) and continue the process.

In case we end up with a cell that already has a number we instead place our next number in the cell immediately below the current cell. This rule also applies if you are in a corner and exit out of both columns and rows.

Now let's code our program in Python! The first part of our code asks the user for dimensions for the square as well as our starting number (remember that this will be placed in the first row, middle column).

We use numpy as the library of choice for storing our arrays in this program.

import numpy as np

dimension = int(input("Choose a size for this magic square 
            (please enter an odd number): " ))
number = float(input("Choose a starting number for your 
            magic square: "))

Next, in the below code we use numpy to create a two dimensional array (as to make a square) with the dimensions of the user's input and then make a second array for storing presence/absence values. We then check if our starting number is an integer and if it is, make the numpy array an integer array and to change our starting number which was a float to an integer.

# create magic square array and a duplicate for comparison
magic_square = np.zeros([dimension, dimension], dtype = int)
fill_checker = np.zeros([dimension, dimension])

rounded = round(number)

if (rounded == number):
      number = round(number)
      np.int_(magic_square)

Then we initialize the magic square by placing the starting number in the first row, middle column.

# place the first number in the top row, middle column
right = int((dimension-1)/2)
up = 0
magic_square[up][right] = number
fill_checker[up][right] = 1

Next, we create a function that checks for various cases and places the next number in the appropriate cell.

# the below function will take the current position
# i.e., num in position (x,y) and 
# will determine where to place num+1
def find_next_pos (x,y,num):

      global number
      global up
      global right

      if (x + 1 > dimension - 1 and y - 1 < 0):
            #check if the position is going off 
            #both the row and column ranges
            #in which case we simply place the 
            #next number in the cell below

            magic_square[y+1][x] = num + 1
            fill_checker[y+1][x] = 1
            up = y + 1
            right = x
            number += 1

      elif (x + 1 > dimension - 1):
            #check if you are going off the column range

            magic_square[y-1][x - (dimension - 1)] = num + 1
            fill_checker[y-1][x - (dimension - 1)] = 1
            up = y - 1
            right = x - (dimension - 1)
            number += 1

      elif (y - 1 < 0):
            #check if you are going off the row range

            magic_square[y+dimension-1][x+1] = num + 1
            fill_checker[y+dimension-1][x+1] = 1
            up = y + dimension-1
            right = x + 1
            number += 1

      else:
        #we are now within the square and not going out

            if (fill_checker[y-1][x+1] == 0):  
              #check if you can go normal diagonal into an empty cell

              magic_square[y-1][x+1] = num + 1
              fill_checker[y-1][x+1] = 1
              up = y-1
              right = x + 1
              number += 1

            else:
              #this situation means that the diagonal 
              #position is occupied

              magic_square[y+1][x] = num + 1
              fill_checker[y+1][x] = 1
              up = y + 1
              right = x
              number += 1

The final step in our code uses our function we just created dimension ^2 times and then prints the numbers from the array one by one with dashes and other characters to represent the lines in an actual magic square. After this you are done!

# we now are ready to call the above 
# function to populate the full magic square
for i in range(1,dimension*dimension):
      find_next_pos(right, up, number)

# Now we are ready to pretty print the full array
top = "-"*(dimension*(len(str(number))+1)+1)
print(top)
spacing = '{:'+ str(len(str(number))) + '}'

for i in range(len(magic_square)) : 
      print("|", end = "")
      for j in range(len(magic_square[i])) :
      print (spacing.format(magic_square[i][j]), end='')
      print("|", end = "")
      print()

print(top)

Let us try to generate a 3-by-3 magic square:

Choose a size for this magic square (please enter an odd number): 3
Choose a starting number for your magic square: 1
-------
|8|1|6|
|3|5|7|
|4|9|2|
-------

Here is what the program generates when we attempt a 11-by-11 magic square:

Choose a size for this magic square (please enter an odd number): 11
Choose a starting number for your magic square: 99
---------------------------------------------
|166|179|192|205|218| 99|112|125|138|151|164|
|178|191|204|217|109|111|124|137|150|163|165|
|190|203|216|108|110|123|136|149|162|175|177|
|202|215|107|120|122|135|148|161|174|176|189|
|214|106|119|121|134|147|160|173|186|188|201|
|105|118|131|133|146|159|172|185|187|200|213|
|117|130|132|145|158|171|184|197|199|212|104|
|129|142|144|157|170|183|196|198|211|103|116|
|141|143|156|169|182|195|208|210|102|115|128|
|153|155|168|181|194|207|209|101|114|127|140|
|154|167|180|193|206|219|100|113|126|139|152|
---------------------------------------------

Interested in more things Python? Checkout our post on Python queues. Also see our blogpost on Python's enumerate() capability. Also if you like Python+math content, see our blogpost on finding the prime factorization of a number. Finally, master the Python print function!

Want to learn Python with us? Sign up for 1:1 or small group classes. Also checkout our blogpost on Fibonacci numbers.