Kodeclik Blog
Numbered squares from 1 to 100
Python is a very handy tool to do simple arithmetic for us. We can write simple programs to search through numbers for those that have specific properties. For instance, let us suppose we wish to find all the numbered squares from 1 to 100. In other words, we wish to find numbers in the range [1,100] that are squares of other numbers.
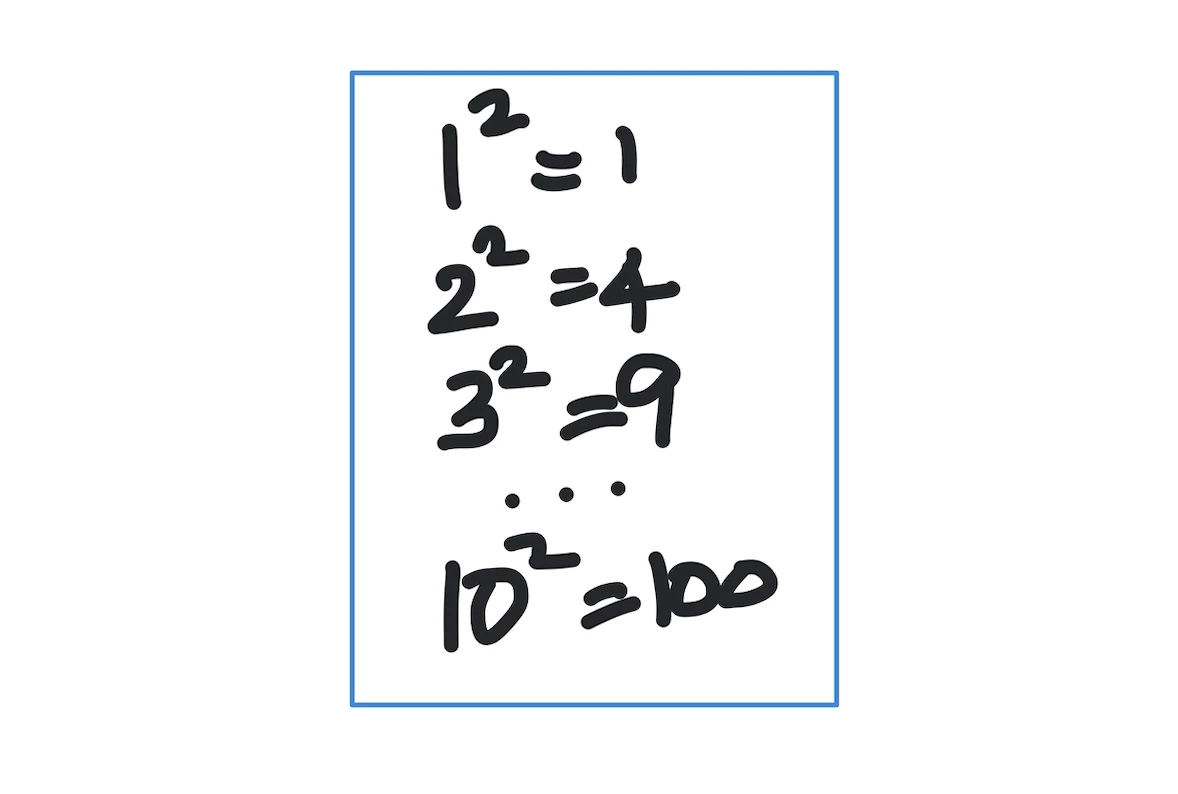
One way to do it is to realize that 1 squared is 1 and 10 squared is 100, so the square numbers we are looking for are simply squares of numbers from 1 to 10. Here is a simple Python program to do the task for us:
for i in range(10):
print(str(i+1) + "\\tsquared is " + str((i+1)*(i+1)) + ".")In this program we create a for loop that cycles through 10 values (the argument of the range function). Typically a for loop begins from 0 to one less than the range’s argument, i.e., from 0 to 9 in our case. So we add 1(i+1) so that the loop really goes from 1 to 10. Inside the for loop we print the square of this number in a pretty format.
The output is:
1 squared is 1.
2 squared is 4.
3 squared is 9.
4 squared is 16.
5 squared is 25.
6 squared is 36.
7 squared is 49.
8 squared is 64.
9 squared is 81.
10 squared is 100.The same program could also have been written as:
for i in range(1,11):
print(str(i) + "\\tsquared is " + str((i)*(i)) + ".")Note that the range now begins with 1 and will end at 10 because the second argument to the range function is 11, which is one more than what we need. The output will be the same as before:
1 squared is 1.
2 squared is 4.
3 squared is 9.
4 squared is 16.
5 squared is 25.
6 squared is 36.
7 squared is 49.
8 squared is 64.
9 squared is 81.
10 squared is 100.A second way to find numbered squares from 1 to 100 is to cycle through all numbers from 1 to 100 checking if each is a square. Here is how that would work:
for i in range(1,101):
s = int(i**0.5)
if (s*s == i):
print (str(i) + "\\t is a perfect square, and is "
+ str(s) +" squared.")Here we cycle through the numbers from 1 to 100. At each step we find its square root using the exponentiation operator. Note that the square root need not be an integer (e.g., the square root of 2 is an irrational number that goes 1.414.2135..) We convert this to an integer using the int() function. Then we ask if that integer squared (i.e., s squared) gives us back the original number (i.e., i). If so, then we can be sure we have hit upon a square. The output will be:
1 is a perfect square, and is 1 squared.
4 is a perfect square, and is 2 squared.
9 is a perfect square, and is 3 squared.
16 is a perfect square, and is 4 squared.
25 is a perfect square, and is 5 squared.
36 is a perfect square, and is 6 squared.
49 is a perfect square, and is 7 squared.
64 is a perfect square, and is 8 squared.
81 is a perfect square, and is 9 squared.
100 is a perfect square, and is 10 squared.Thus we have a very handy Python approach to find numbered squares for us in a given range. Experiment with it by changing the range and finding higher square numbers! Or to make things more interesting, use it to find numbered cubes!
For more Python content, checkout the math.ceil() and math.floor() functions! Also
learn about the math domain error in Python and how to fix it!
Interested in more things Python? Checkout our post on Python queues. Also see our blogpost on Python's enumerate() capability. Also if you like Python+math content, see our blogpost on Magic Squares. Finally, master the Python print function!
Want to learn Python with us? Sign up for 1:1 or small group classes.