Kodeclik Blog
Pick's Theorem: A Simple Formula for Polygon Areas
Pick's Theorem provides an elegant method to calculate the area of polygons whose vertices lie on lattice points (points with integer coordinates). It is cool because it works even if the shape of the polygon is not a well known shape like a rectangle or a triangle.
Pick’s theorem is expressed by the formula:
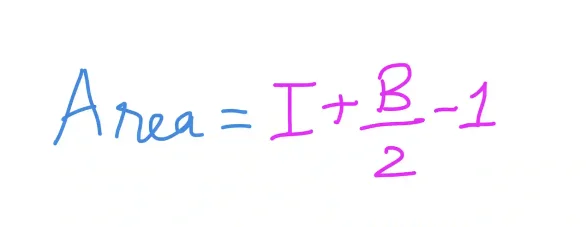
where I is the number of lattice points inside the polygon and B is the number of lattice points on the boundary of the polygon.
Learn Pick's theorem by interactively creating a four cornered shape in the grid below and see how it calculates the area below! Go ahead - try it!
This program is an interactive tool that helps you learn about Pick's Theorem, a way to calculate the area of a polygon drawn on a grid. It uses a grid of dots where you can place four points to form the corners of a polygon. Once you've placed the corners, the program calculates the area, the number of boundary points, and the number of interior points.
When you click on the canvas, it places a corner of your polygon at the nearest dot. You can place up to four corners. If you want to change a corner's position, you can drag it to a new location. The shape of the polygon updates automatically, and the program recalculates the area and other details each time.
Here is an example of a polygonal area calculation using our interface:
When does Pick’s theorem work?
Pick’s theorem works for any polygon with vertices on lattice points, including both convex and non-convex shapes. It elegantly combines discrete counting of points with continuous geometric area calculation. This theorem simplifies area calculations for irregular shapes that would otherwise require complex integration or calculus.
Pick’s theorem specifically requires the polygon to be "simple," meaning it must not have any self-intersection. A simple polygon is one where:
Why does Pick’s theorem work?
The proof of Pick's Theorem follows a systematic approach. We will not prove it here but will suggest the outlines of the proof. First, prove the theorem for elementary triangles (triangles with no lattice points except vertices).Then extend the proof to arbitrary triangles with lattice point vertices. Finally, prove it for any polygon by showing that: (i) any polygon can be split into triangles, and (ii) if the theorem holds for two adjacent polygons, it holds for their combination as well!
Pick's Theorem does not directly extend to polygons with non-integer coordinates, but it has several important variations and generalizations such as polygons with holes! Also note that Pick's Theorem cannot be directly applied to self-intersecting polygons. The conditions stated above should be satisfied (which are violated in the case of self-intersecting polygons).
Summary
Pick's Theorem is a mathematical formula that calculates the area of a polygon with vertices on lattice points (integer coordinates) using the formula A = I + B/2 - 1, where I is the number of interior lattice points and B is the number of boundary points. The theorem works for both convex and non-convex shapes, making it a powerful tool for calculating areas of irregular polygons without requiring complex calculus.
While Pick's Theorem is elegant in its simplicity for 2D integer lattices, it has significant limitations. It cannot be directly extended to polygons with non-integer coordinates or self-intersecting polygons, though modifications exist for special cases like polygons with holes.
