Kodeclik Blog

Solving the Tower of Hanoi in Python

What is the Tower of Hanoi?

The Tower of Hanoi is a classical mathematical puzzle formulated by Édouard Lucas, a French mathematician and is believed to have origins in mythological stories, variously about Indian temples or monasteries in Vietnam. As legend goes, the puzzle lays out the rules of the game which are to be followed by priests and solving the puzzle is intended to increase the mental faculties of young priests.

What are the rules of Tower of Hanoi?

There are many variants of the Tower of Hanoi puzzle and the classical version has 3 pegs and 3 disks (of varying sizes, arranged in order), as shown below (top). The goal of the puzzle is to get these disks from the left peg to the right peg, as shown in the bottom panel of the figure.

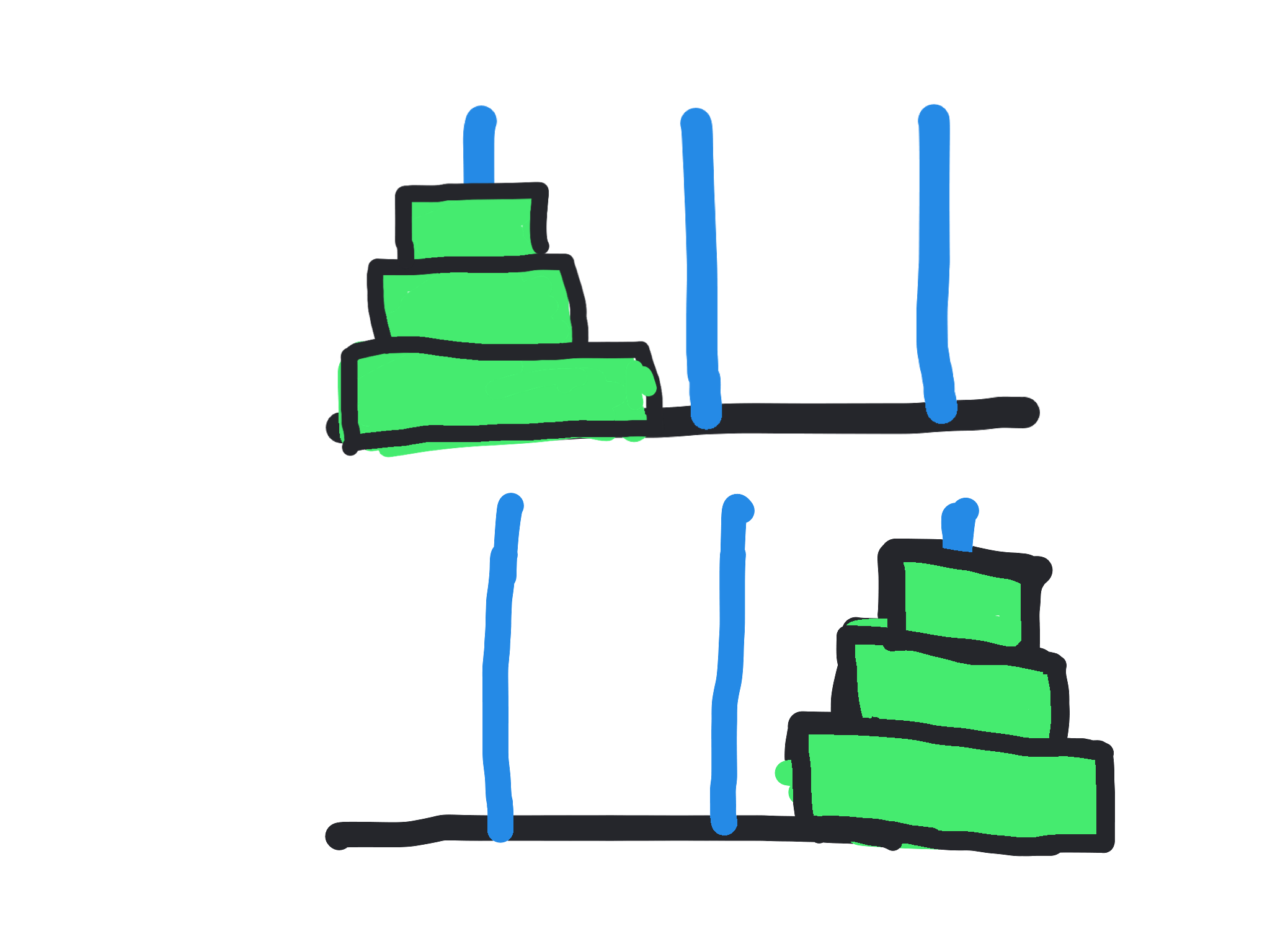
But there are some rules to the game. One, we can only move only disk at a time. Second, in each step, we can only move the disk that is on top of some peg (i.e., the disk that is not obstructed by another desk). Finally, and most importantly, a larger disk cannot be placed on top of a smaller disk.

Is the Tower of Hanoi solvable?

Yes, the Tower of Hanoi is a solvable problem and there are many elegant ways to solve it.

How many steps does it take to solve the Tower of Hanoi?

For 3 pegs and n disks, we can show that it can be solved in (2^n)-1 steps. For instance, assume we have 2 disks for simplicity (but 3 pegs, as standard). The way to solve it is to move the smaller disk to the middle peg, the larger one to the right peg and put back the smaller disk on top of the larger disk. This takes 3 steps, as estimated earlier. With 3 disks, we can solve it in 7 steps, and so on.

How can we solve the Tower of Hanoi puzzle?

There is a very classical recursive solution to the Tower of Hanoi puzzle. It works as follows. Given the original position, assume that we have somehow (suspend disbelief for a moment) moved n-1 disks to the middle peg in the correct order. We can then move the largest disk to the right peg and then (somehow, again) move the n-1 disks from the middle peg to the right peg. We are in essence using the middle peg as an intermediate/temporary peg in the path from the left peg to the right peg.

You might ask: how do we move (n-1) disks as promised earlier (in two steps)? We solve it recursively! We assume we somehow move (n-2) disks, only this time using the right peg as the temporary peg (because the middle peg is the intended destination for n-1 pegs), and continue the recursive pattern.

Python code to solve the Tower of Hanoi

Here is Python code to solve the Tower of Hanoi puzzle. As you can see it is really short spending the bulk of its time in recursive calls. It also counts the number of steps taken and prints the steps.

def tower_of_hanoi(disks,start,end,intermediate):
steps = 0;
if (disks == 1):
  print("Move disk from peg:",start,"to peg:",end)
  steps += 1
else:
  steps += tower_of_hanoi(disks-1,start,intermediate,end)
  print("Move disk from peg:",start,"to peg:",end)
  steps += 1
  steps += tower_of_hanoi(disks-1,intermediate,end,start)
return(steps)

We can invoke this function as follows:

operations = tower_of_hanoi(4,"left","right","middle")
print("This took",operations,"steps.")

The output is:

Move disk from peg: left to peg: middle
Move disk from peg: left to peg: right
Move disk from peg: middle to peg: right
Move disk from peg: left to peg: middle
Move disk from peg: right to peg: left
Move disk from peg: right to peg: middle
Move disk from peg: left to peg: middle
Move disk from peg: left to peg: right
Move disk from peg: middle to peg: right
Move disk from peg: middle to peg: left
Move disk from peg: right to peg: left
Move disk from peg: middle to peg: right
Move disk from peg: left to peg: middle
Move disk from peg: left to peg: right
Move disk from peg: middle to peg: right
This took 15 steps.

If you enjoyed the recursion in the Tower of Hanoi puzzle, checkout our blogposts on merge sort and quicksort. Also learn about Python's enumerate() functionality.

Want to learn Python with us? Sign up for 1:1 or small group classes.